Liouville's theorem ↩

Metadata

aliases: []
shorthands: {}
created: 2022-05-28 14:02:51
modified: 2022-05-28 14:26:36

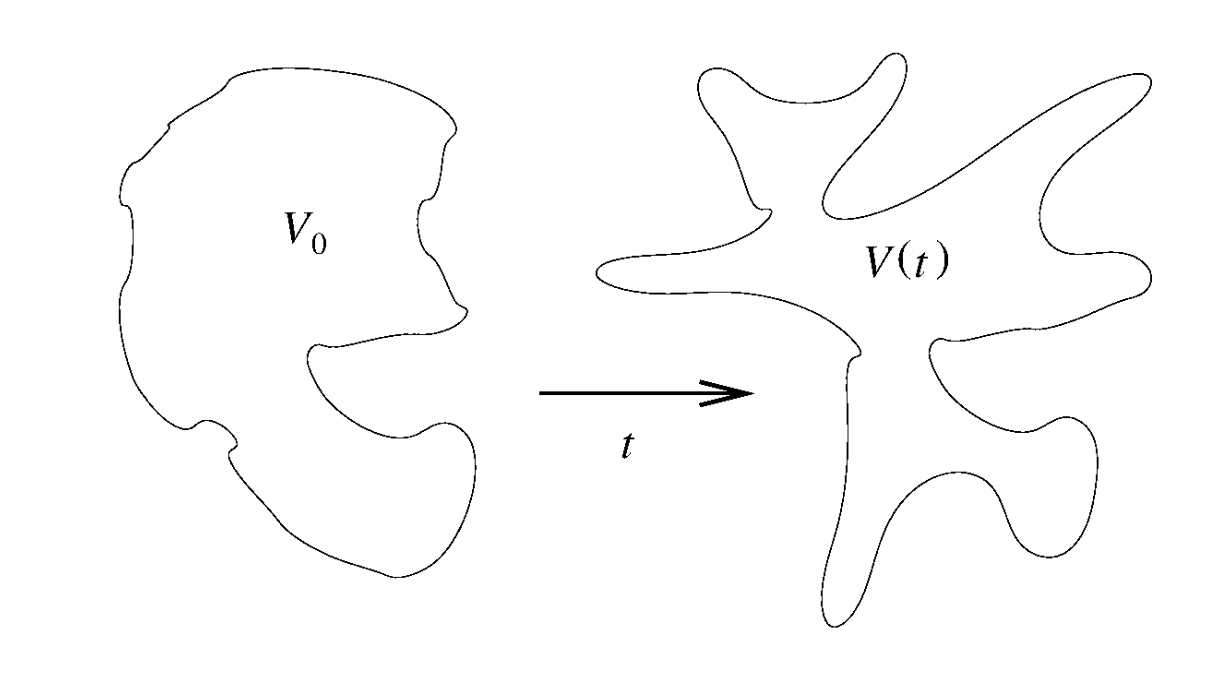
Liouville's theorem states that in Hamiltonian mechanics, an arbitrary

subset of the phase space

seen as a set of initial conditions

retains its volume through time development:

Proof

Let the physical system in question have degrees of freedom.
Also, let be the velocity space inside the phase space, meaning that we assign a dimensional vector to each point of the dimensional phase space:

Where the dots mean the time derivatives.

Then take the divergence of :

Where we substituted the canonical equations (see Hamiltonian mechanics) which made the individual contents in the sum zero.

Due to the divergence theorem, this means that considering an arbitrary segment of the phase space, the "flow" described by takes just as much "stuff" out as it is taking in. This is analogous to incompressible fluids, where the volume remains the same.